Tim Gowers - Computational Complexity and Quantum Compuation
| Created: | 2009-04-26 22:08 |
|---|---|
| Institution: | Department of Applied Maths and Theoretical Physics |
| Editors' group: | (not set) |
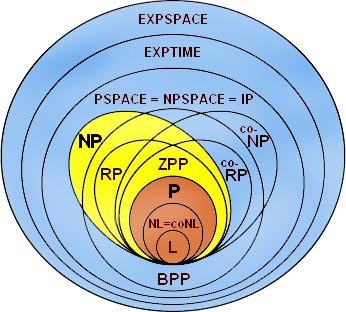
| Description: | Computational complexity is the study of what resources, such as time and memory, are needed to carry out given computational tasks, with a particular focus on lower bounds for the amount needed of these resources. Proving any result of this kind is notoriously difficult, and includes the famous problem of whether P = N P . This course will be focused on two major results in the area. The first is a lower bound, due to Razborov, for the number of steps needed to determine whether a graph contains a large clique, if only “monotone” computations are allowed. This is perhaps the strongest result in the direction of showing that P and N P are distinct (though there is unfortunately a very precise sense in which the proof cannot be developed to a proof of the whole conjecture). The second is Peter Shor’s remarkable result that a quantum computer can factorize large integers in
polynomial time. In order to present these two results, it will be necessary to spend some time discussing some of the basic concepts of computational complexity, such as the relationship between Turing machines and the more obviously mathematical notion of circuit complexity, and an introduction to what a quantum computation actually is. For the latter, no knowledge of quantum mechanics will be expected, and scarcely any will be imparted during the course: it is possible to understand quantum computation in a very “pure mathematics” way. The reason this is a graduate course rather than a Part III course is that I intend to give several lectures in an informal style that would be hard to examine. It is not because the material will be more advanced: indeed, my aim will be to make allowances for the fact that people will not be working on it with an exam in mind, and to make the course as easy to follow as I can. Having said that, the main results will be proved in full: the informal discussion will be with a view to making these proofs more comprehensible. The collection will have 12 graduate level lectures which are currently being given during the Easter term 2009. Many thanks to Adrian Callum-Hinshaw for his help with these video lectures. |
Media items
This collection contains 10 media items.
Media items
Gowers Lecture 01
15,971 views
Equivalence between Turing machines and the circuit model of compuation
Collection: Tim Gowers - Computational Complexity and Quantum Compuation
Institution: Department of Applied Maths and Theoretical Physics
Created: Wed 6 May 2009
Gowers Lecture 10
2,065 views
Final details needed for the quantum Fourier transform, such as how to "uncompute".
Solving the descrete logirithm problem.
Collection: Tim Gowers - Computational Complexity and Quantum Compuation
Institution: Department of Applied Maths and Theoretical Physics
Created: Wed 3 Jun 2009
Gowers Lecture 2
5,445 views
Definition of P, NP and NP-complete and some examples.
Collection: Tim Gowers - Computational Complexity and Quantum Compuation
Institution: Department of Applied Maths and Theoretical Physics
Created: Mon 4 May 2009
Gowers Lecture 3
6,999 views
A demonstration that clique is NP-complete, and some lower bound complexity proofs which don't work.
Collection: Tim Gowers - Computational Complexity and Quantum Compuation
Institution: Department of Applied Maths and Theoretical Physics
Created: Mon 4 May 2009
Gowers Lecture 4
2,529 views
Part I of Razborov's proof that no monotone circuit can solve Clique in polynomial time
Collection: Tim Gowers - Computational Complexity and Quantum Compuation
Institution: Department of Applied Maths and Theoretical Physics
Created: Mon 4 May 2009
Gowers Lecture 5
2,115 views
Part II of Razborov's proof that Clique cannot be solved in polynomial time by monotone circuits
Collection: Tim Gowers - Computational Complexity and Quantum Compuation
Institution: Department of Applied Maths and Theoretical Physics
Created: Tue 5 May 2009
Gowers Lecture 6
1,524 views
No "natural proof" exists for proving a separation between P and NP if one-way functions exist. We then move into a mathematician's description of quantum computation starting...
Collection: Tim Gowers - Computational Complexity and Quantum Compuation
Institution: Department of Applied Maths and Theoretical Physics
Created: Mon 11 May 2009
Gowers Lecture 7
2,105 views
Description of quantum computation continued. We start describing Shor's factoring algorithm.
Collection: Tim Gowers - Computational Complexity and Quantum Compuation
Institution: Department of Applied Maths and Theoretical Physics
Created: Mon 11 May 2009
Gowers Lecture 8
1,391 views
Shor's factoring algoirthm continued.
Collection: Tim Gowers - Computational Complexity and Quantum Compuation
Institution: Department of Applied Maths and Theoretical Physics
Created: Wed 3 Jun 2009
Gowers Lecture 9
1,702 views
Shor's Algorithm continued
Collection: Tim Gowers - Computational Complexity and Quantum Compuation
Institution: Department of Applied Maths and Theoretical Physics
Created: Wed 3 Jun 2009